Logarithmische Skalen und geometrisches Mittel

Wenn man sich – so wie ich derzeit – auf eine Amateurfunkprüfung vorbereitet, stolpert man auch über das ein oder andere Diagramm mit logarithmischen Achsen. Ein Beispiel ist die Grafik zum Thema Kabeldämpfungen, bei der sowohl die x-, als auch die y-Achsen logarithmisch sind:

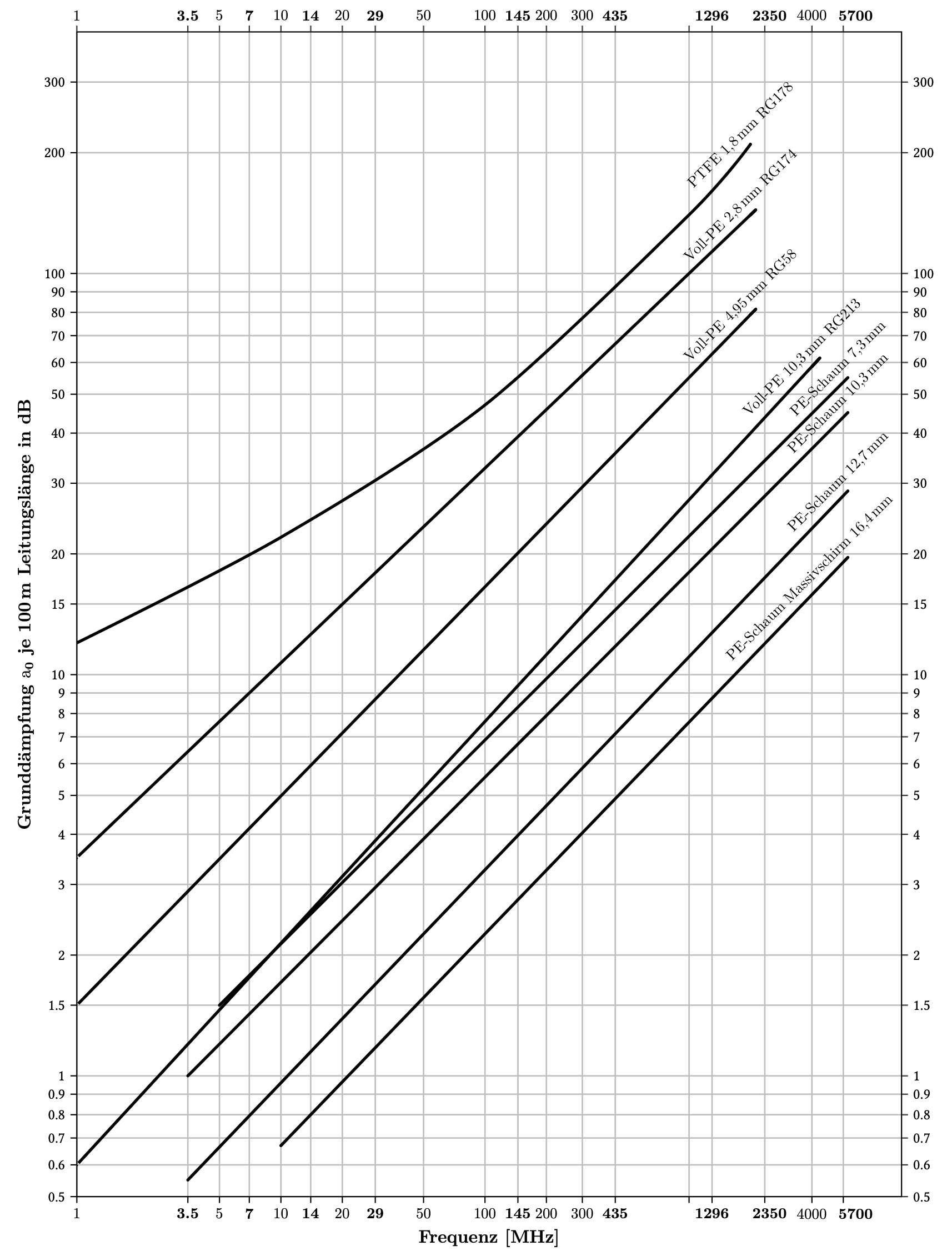
Zwischen zwei Werten liegt?

Neulich stellte sich mir die Frage, welcher Wert wohl auf der x-Achse zwischen der Markierung 50 und der Markierung 100 genau liegt?

Bei einer “normalen”, linearen Skala ist das einfach und jeder weiß sofort: zwischen 50 und 100 liegt 75 – der (arithmetische) Mittelwert, $\frac{50+100}{2}$.

Wie ist das aber bei einer logarithmischen Skala? Die Antwort ist verblüffend: Es ist das geometrische Mittel: $\sqrt{50*100}\approx 70.71$.

Logarithmische Skala

Eine logarithmische Skala ist eine Skala, bei der die Abstände auf der Achse nicht linearen, sondern multiplikativen Beziehungen entsprechen. Das bedeutet, dass gleiche Abstände auf der Skala gleichen Verhältnissen oder Faktoren entsprechen, anstatt gleichen Differenzen.

Beispiel: Auf einer linearen Skala ist der Abstand zwischen 1 und 2 derselbe wie zwischen 2 und 3 (Differenz von 1). Auf einer logarithmischen Skala ist der Abstand zwischen 1 und 10 derselbe wie zwischen 10 und 100 (Faktor von 10).

Mathematisch gesehen wird ein Wert $x$ auf einer logarithmischen Skala durch seinen Logarithmus $log(x)$ dargestellt. Der Abstand zwischen zwei Punkten $x_1$ und $x_2$ auf der logarithmischen Skala ist proportional zu $log(x_2)−log(x_1)$.

Herleitung geometrisches Mittel

Nehmen wir an, wir haben zwei Punkte auf einer logarithmischen Skala, $A$ und $B$. Wir suchen einen Punkt $M$, der genau in der Mitte zwischen $A$ und $B$ liegt. Auf einer linearen Skala würde der Mittelpunkt $M_{linear}$ durch den arithmetischen Mittelwert gefunden: \(M_{linear} = \frac{A+B}{2}\)

Auf einer logarithmischen Skala ist der “Abstand” zwischen den Punkten jedoch durch die Logarithmen ihrer Werte definiert. Wenn $M$ der Mittelpunkt zwischen $A$ und $B$ auf der logarithmischen Skala ist, dann muss der logarithmische Abstand von $A$ zu $M$ gleich dem logarithmischen Abstand von $M$ zu $B$ sein.

Das bedeutet: \(log(M)−log(A)=log(B)−log(M)\)

Jetzt können wir diese Gleichung nach $M$ auflösen:

\[\begin{align*} & \qquad & log(M) - log(A) &=\; log(B) - log(M) && \quad |\, +log(M) \\ &\Leftrightarrow \qquad & 2 \cdot log(M) - log(A) &=\; log(B) && \quad |\, +log(A) \\ &\Leftrightarrow \qquad & 2 \cdot log(M) &=\; log(A) + log(B) && \quad |\, \text{1. Logarithmengesetz} \\ &\Leftrightarrow \qquad & 2 \cdot log(M) &=\; log(A \cdot B) && \quad |\, \text{3. Logarithmengesetz} \\ &\Leftrightarrow \qquad & log(M^2) &=\; log(A \cdot B) && \quad |\, 10^{x} \\ &\Leftrightarrow \qquad & M^2 &=\; A \cdot B && \quad |\, \sqrt{} \\ &\Rightarrow \qquad & M &=\; \sqrt{A \cdot B} && \end{align*}\]

Jetzt können wir also leicht immer die Mitte zwischen zwei Markierungen auf logarithmischen Achsen finden.

Noch ein Beispiel zur Grafik oben: Genau auf der halben Strecke zwischen 100 und 200 auf der y-Achse liegt also der Wert $\sqrt{100\cdot200}\approx 141.4$.

Auf der x-Achse ist zwischen 100 und 200 die 145 markiert – wenn man genau hinschaut, sieht man auch, dass der 145er Strich nicht exakt in der Mitte zwischen 100 und 200 liegt, sondern korrekterweise einen Hauch weiter rechts.

🔲